I kicked off the level 5 Google Foobar problem, and wow, what a fantastic finale! This was the question:
Dodge the Lasers!
=================
Oh no! You've managed to escape Commander Lambda's collapsing space station in an escape pod with the rescued bunny workers - but Commander Lambda isnt about to let you get away that easily. Lambda sent an elite fighter pilot squadron after you -- and they've opened fire!
Fortunately, you know something important about the ships trying to shoot you down. Back when you were still Commander Lambdas assistant, she asked you to help program the aiming mechanisms for the starfighters. They undergo rigorous testing procedures, but you were still able to slip in a subtle bug. The software works as a time step simulation: if it is tracking a target that is accelerating away at 45 degrees, the software will consider the targets acceleration to be equal to the square root of 2, adding the calculated result to the targets end velocity at each timestep. However, thanks to your bug, instead of storing the result with proper precision, it will be truncated to an integer before adding the new velocity to your current position. This means that instead of having your correct position, the targeting software will erringly report your position as sum(i=1..n, floor(i*sqrt(2))) - not far enough off to fail Commander Lambdas testing, but enough that it might just save your life.
If you can quickly calculate the target of the starfighters' laser beams to know how far off they'll be, you can trick them into shooting an asteroid, releasing dust, and concealing the rest of your escape. Write a function solution(str_n) which, given the string representation of an integer n, returns the sum of (floor(1*sqrt(2)) + floor(2*sqrt(2)) + ... + floor(n*sqrt(2))) as a string. That is, for every number i in the range 1 to n, it adds up all of the integer portions of i*sqrt(2).
For example, if str_n was "5", the solution would be calculated as
floor(1*sqrt(2)) +
floor(2*sqrt(2)) +
floor(3*sqrt(2)) +
floor(4*sqrt(2)) +
floor(5*sqrt(2))
= 1+2+4+5+7 = 19
so the function would return "19".
str_n will be a positive integer between 1 and 10^100, inclusive. Since n can be very large (up to 101 digits!), using just sqrt(2) and a loop won't work. Sometimes, it's easier to take a step back and concentrate not on what you have in front of you, but on what you don't.
Languages
=========
To provide a Java solution, edit Solution.java
To provide a Python solution, edit solution.py
Test cases
==========
Your code should pass the following test cases.
Note that it may also be run against hidden test cases not shown here.
-- Java cases --
Input:
Solution.solution('77')
Output:
4208
Input:
Solution.solution('5')
Output:
19
-- Python cases --
Input:
solution.solution('77')
Output:
4208
Input:
solution.solution('5')
Output:
19
Use verify [file] to test your solution and see how it does. When you are finished editing your code, use submit [file] to submit your answer. If your solution passes the test cases, it will be removed from your home folder.
That hint deserved some focus: “Sometimes, it’s easier to take a step back and concentrate not on what you have in front of you, but on what you don’t.” My first thought was to focus on the error component. The answer to the step function is what they’re asking for, but maybe I could use calculus to instead get the accurate answer. Then I could step back from the accurate answer by the amount of error. We know that the position is the integral of velocity, and velocity the integral of acceleration, so then the accurate answer must be given by ( ( sqrt2/2 ) * t^2 ). I put that in a table vs the step function alongside the difference/error:
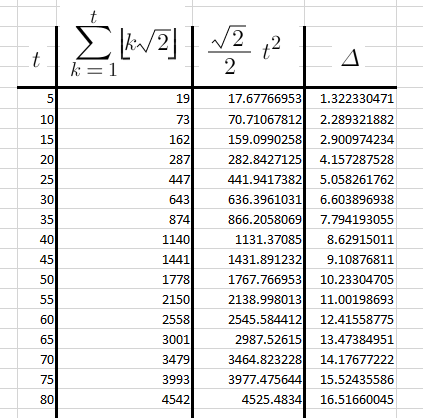
I was hoping that I might see a pattern, some way to generate the amount of error as a predictable function of time. Then we could take the accurate answer, step away from that by the amount of error, and instantly get the answer without any looping. But alas, if there is a pattern there, I wasn’t able to see it.
Next I focused on visualizing the acceleration as a triangle. The question did mention the acceleration was at 45 degrees, so the opposite and adjacent sides must each be increasing by 1 each time step. So I tried working with those components individually thinking they might be easier to work with, and then I could combine them back at the end. I tried playing with different trig functions. I even tried polar coordinates. I had a lot of fun revisiting mathematical tools I hadn’t used in a long time, but unfortunately nothing here got me closer to a solution.
Next I started to read up on the floor function. Maybe it had some quirks that would be useful. One formula quickly caught my attention:
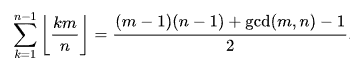
If I wanted the solution of the step function at t, then I could just make n = t+1 and m = (t+1)*sqrt2. It technically only applies to integers, but it is possible to use the Euclidean algorithm to get the gdc of real numbers. Would that work? It actually does to a point, many of the tests started passing when I did this. But some of them failed, and it soon became clear that this approach wasn’t going to work.
This was the next formula to catch my attention:
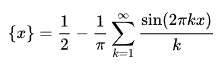
So the fractional component of the floor could be expressed as a Fourier expansion! Then our step function could become:
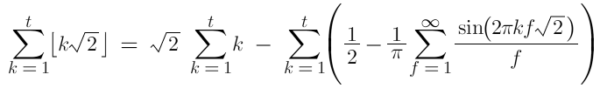
The integer part could turn into a simple triangular number series, and I already knew that Google was fond of the triangular series. The first portion of the fractional part turns into simple multiplication, so the remaining Fourier series was the only complexity. I suspected the frequency components might turn out to cancel each other out, perhaps combine, or have some other interesting behaviour that would cause it to simplify. This was a lot of a fun, but once again, turned out to be a dead end. This didn’t simplify things at all.
Although the Fourier trials weren’t successful, they had gotten me thinking of the triangular numbers. If the acceleration had been 1 then the answer would be a straight triangular series. But ours is sqrt2 so we have gaps, but maybe I could focus on the gaps instead of the step function itself. The function for the gaps might simplify easier than our desired step function, and if it does then our answer could be obtained by taking the unit acceleration minus the gaps. I visualized the step function on a number line, both before and after the floor takes place. A few things really stand out. First, prior to the affect of the floor function the rate is constant. Second, we can see that each step of our position function will either produce an answer that is one integer higher than the prior step, or it will be two more if the prior value was within (1 - sqrt2) of the next. Since sqrt2 is less than two we know it will never be able to jump more than one integer.
Since the rate is constant, if we had an acceleration value that was set in the first gap and that was behind the step function by the same amount that the floor pulls it back, then it would be the same relative distance behind while also increasing at a constant rate, so it would then hit every gap. The first gap was at 3sqrt2, and the prior steps value was being pulled back by the floor function a distance of (2sqrt2 - 2). So ( 3sqrt2 - (2sqrt2 - 2) ) is the acceleration that would hit every gap. But would that function actually simplify easier?
I visualized an example at a time of 8:
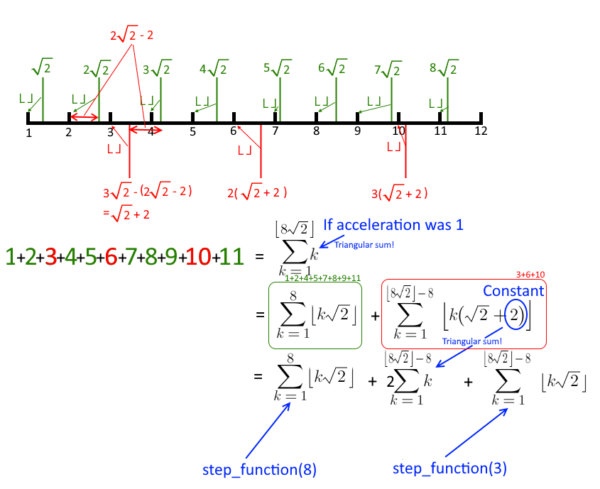
So we know the unit acceleration would have stopped at a time of floor(8sqrt2). And we know that there must be ( floor(8sqrt2) - 8 ) gaps. So we know the unit acceleration is equal to our desired step function plus our new gap function at a time of ( floor(8sqrt2) - 8 ). But something interesting becomes apparent when writing this out: the constant component pulls out of the floor function since it has no fractional part. It just turns into another triangular series. What it leaves behind is our same step function, just now it is reduced to a time of ( floor(8sqrt2) - 8 ).
I was hoping the function for the gaps might simplify to allow us an instant answer by subtracting it from the unit acceleration. That didn’t happen. But this reduction in time step input still might help. Does it help enough? It is reducing us from our inputTime to a new time of ( floor(inputTime*sqrt2) - inputTime ). The floor is going to change it by less than one, so we are reducing by a factor of roughly inputTime / (inputTime*sqrt2 - inputTime) = 1/(sqrt2 - 1) = 2.4 How many times would we need to repeat that to reach an answer in the worst case? Our max input is a Googol ( I see what you did there, Google! ). That is 10^100, so if we could reduce the time step input by half each iteration then we would need to repeat this for log2(10^100)=332 iterations. That is already well within the Python recursion limit of 1000, and our reduction is a bit better than that at 2.4. So, yes, using this will work!!!
One remaining problem was needing 100 digits of precision. Floating point certainly wouldn’t do. But using a hard coded sqrt2 shifted by 100 decimals, then shifting the decimal back when we’re done, that will do the job.
And so I had what I needed to escape Lambda’s minions:
# Author: Derek Moran, Level 5, Saboteur and Escape Artist for Bunny Planet
# With big kudos to whoever came up with this problem, THANK YOU!
# All of the problems have been fun, but this one was especially so. It was just such an absolute blast :-)
# Date: 18-DEC-2022
def solution(s):
# Your code here
return getTargetPositionAsString( s )
# Given we have:
# - a target with an acceleration of sqrt2
# - the target velocity at each time 'timeStep' is subjected to a floor() operation
#
# Then returns the position of the target at the given timeStep
# ie: floor(sqrt2) + floor(2sqrt2) + ... + floor(timeStep*sqrt2)
#
# The input timeStepAsString must be a postive integer ( passed as string ) between 1 and 1e100 inclusive
def getTargetPositionAsString( timeStepAsString ):
validationError = "timeStepAsString must be a postive integer ( passed as string ) between 1 and 1e100 inclusive"
if not type(timeStepAsString) is str or not timeStepAsString.isdigit():
raise Exception( validationError )
timeStep = int(timeStepAsString)
if timeStep < MIN_TIME_STEP or timeStep > MAX_TIME_STEP:
raise Exception( validationError )
return str( getTargetPosition( timeStep ) )
def getTargetPosition( timeStep ):
if timeStep == 0: return 0
# We won't have enough precision if we work in floating point
# So we use an integer with the decimal shifted by the max possible timeStep
# Since shifting it back cuts off the decimal portion we will end up with a precise floor( timeStep*sqrt2 )
velocityAtTimeStep = ( timeStep * SQRT2_x_MAX_TIME_STEP ) // MAX_TIME_STEP
# If the target had been accelerating at 1 unit/time, then it would reach the same velocity at this time step
timeStepIfUnitAcceleration = velocityAtTimeStep
# Since unit acceleration would result in the triangular sum we can quickly have a position for this case
positionIfUnitAcceleration = ( timeStepIfUnitAcceleration * ( timeStepIfUnitAcceleration + 1 ) ) >> 1
# But OUR target is accelerating faster than 1 unit/time, at sqrt2 unit/time
# So it will have gaps any time the velocity of prior step is within ( 1 - sqrt2 ) of the next integer
# sqrt2 is less than 2 though, and the floor will be pulling it back each step
# So we know it will never have a gap of more than 1 unit per timeStep
# Therefore we know how many gaps will exist as compared to our 1 unit/time acceleration case
numGapsFromUnitAcceleration = timeStepIfUnitAcceleration - timeStep
# Focus on where the first gap happens; when it goes from 2sqrt2 to 3sqrt2
# We can see that 2sqrt2 will be ahead of 2 by ( 2sqrt2 - 2 ) before the floor pulls it back
# What if a target was accelerating such that its position was this same distance behind the next?
# Such a target must hit every gap since it will always be the same relative distance behind
# The next is 3sqrt2, so this acceleration that would hit the gaps is 3sqrt2 - ( 2sqrt2 - 2 ) = sqrt2 + 2
# The velocity would then be floor(timeStep*(sqrt2 + 2))
# But floor(timeStep*(sqrt2 + 2)) = floor(timeStep*sqrt2) + 2*timeStep, since there is no decimal part to 2*timeStep
# So our position for a target accelerating such that it hits all the gaps is then:
# positionIfGapAcceleration
# = floor(sqrt2) + floor(2sqrt2) + ... + floor(numGapsFromUnitAcceleration*sqrt2)
# + 2*( 1 + 2 + ... + numGapsFromUnitAcceleration )
# The first part is our original position function, but at a time step of numGapsFromUnitAcceleration
positionIfGapAcceleration = getTargetPosition( numGapsFromUnitAcceleration )
# And the second part is just 2 more triangular series that we can easily calculate
positionIfGapAcceleration += numGapsFromUnitAcceleration * ( numGapsFromUnitAcceleration + 1 )
# We know that our target position is the unit acceleration position minus any gaps
# And we now have that position of a target that is accelerating such that it hits all the gaps
# So, we have an answer!
targetPosition = positionIfUnitAcceleration - positionIfGapAcceleration
# This has reduced us from a time of 'timeStep' to a time of 'numGapsFromUnitAcceleration'
#
# numGapsFromUnitAcceleration
# = timeStepIfUnitAcceleration - timeStep
# = velocityAtTimeStep - timeStep
# = floor(timeStep*sqrt2) - timeStep
# We know the floor will make a difference of less than 1
# So we are roughly reducing from a time of timeStep to a time of ( timeStep*sqrt2 - timeStep )
#
# timeStep / ( timeStep*sqrt2 - timeStep )
# = 1 / ( sqrt2 - 1 )
# = roughly 2.4
#
# We know our worst case is MAX_TIME_STEP = 1e100
# If we were reducing by factor of 2 then we would need log2(1e100)=332 reductions to get the final answer
# 332 is less than the Python recursion limit of 1000
# We're doing a bit better at factor of 2.4, so we know we can answer the worst case well within the limit
return targetPosition
SQRT2_x_MAX_TIME_STEP = int(
"1"
"41421356237309504880"
"16887242096980785696"
"71875376948073176679"
"73799073247846210703"
"88503875343276415727"
)
MIN_TIME_STEP = 1
MAX_TIME_STEP = 10 ** 100
I’ve REALLY enjoyed all of the Google Foobar problems, but this one was definitely my favourite. I love that it had such a simple and easy to understand goal, yet simultaneously required quite an adventure to find a solution.
Many thanks to everyone at Google who created this Foobar challenge. It was a hilarious story throughout, and all of the problems were incredibly fun to work through.









Leave a Reply